SM4算法详解和实现

背景介绍

SM4是国内第一个商用分组密码标准，又称SMS4

SM是商用的拼音缩写，这是国内目前推广的本土密码算法体系，简称国密算法。
在这个体系里有多种算法，包括 SM1-SM9 九种，每一种各不相同，可以用在多个领域中。比如，SM4是分组密码，SM2是公钥密码，SM3是杂凑算法，可用于数字签名等。它们都是由我国自主设计的。
顺带一提，似乎很多密码相关的作品赛都会要求你必须使用国密算法

现行标准的编号为：GB/T 32907—2016

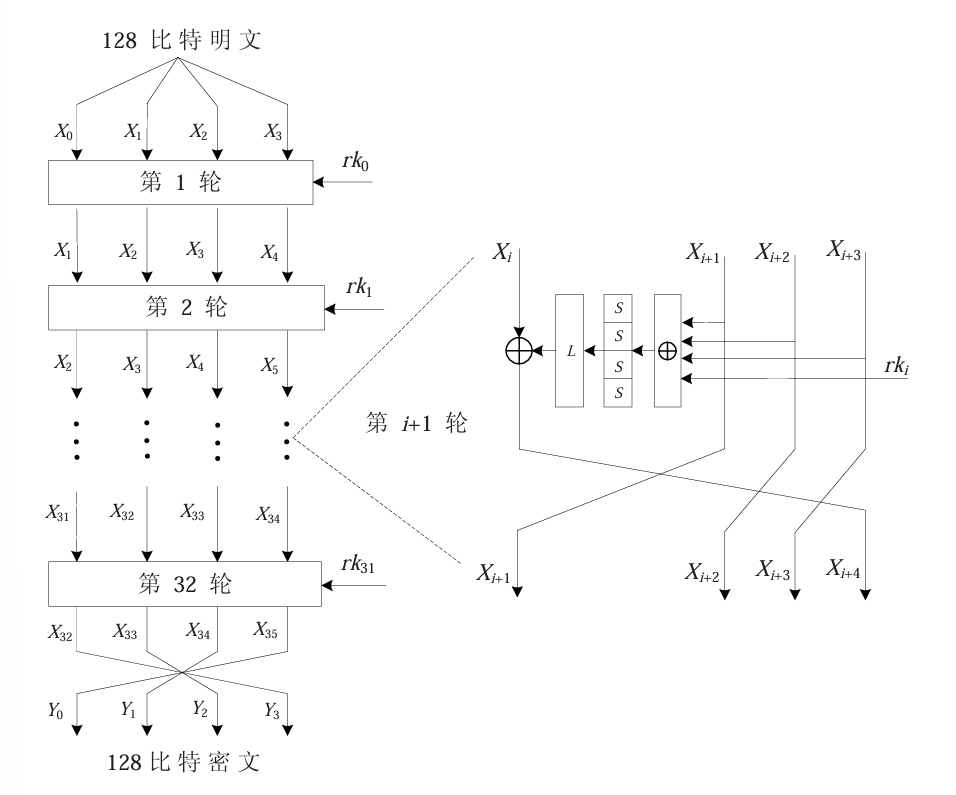
（图片来源：《分组密码的攻击方法与示例分析》）

~~果然分组密码还是得有图才看得懂啊~~

从上图可以看出，SM4的结构还是比较清晰的，而且便于实现，没有太多弯弯绕绕的逻辑（比如IDEA里的那个MA结构）

作为标准的分组密码，它和DES,AES一样，可以被拆分成 整体结构、轮函数、密钥生成函数 这三个部分进行阐释

整体结构

SM4采用的是广义的Feistel结构，每一轮的交换比左右互换稍微更复杂一点，将一组明文分为四组，并在每一轮函数后进行顺序上的交换。

分组长度为128 bit
总共进行32轮
种子密钥长度为128 bit
由种子密钥生成的轮密钥有32个，每个的长度为32 bit

代码示例如下：

class SM4:
	def __init__(self, seedkey: str) -> None:
		self.seedkey = seedkey
		self.subkey = self.genKey()
	
	def Sbox(self, x: str) -> str:
	
	def L(self, x: int) -> int:
	
	def L2(self, x: int) -> int:
	
	def T(self, x: int) -> int:
	
	def T2(self, x: int) -> int:
	
	def genKey(self) -> list:
	
	def rounds(self, text: str, subkey: list) -> str:
	
	def group(self, text: str) -> list:
	
	def encrypt(self, plaintext: str) -> str:
	
	def decrypt(self, ciphertext: str) -> str:

让人疑惑的是为什么该算法的轮数如此之多，其他算法一般都只迭代10-16轮。

轮函数

对于 128 bit 的明文 $X$ ，将其分成4组，每组 32 bit，表示为 $(X_{0}, X_{1}, X_{2}, X_{3})$
相应地，第 $i + 1$ 轮的“明文”可表示为 $(X_{i}, X_{i + 1}, X_{i + 2}, X_{i + 3})$
每一轮的轮密钥长度为 32 bit，将第 $i$ 轮的轮密钥表示为 $r k_{i}$

# 总加密函数
def encrypt(self, plaintext: str) -> str:  
    text = bin(int(plaintext, 16))[2:]  
    if len(text) % 128 != 0:  
        text = text.zfill((len(text) // 128 + 1) * 128)  
  
    groups = self.group(text)  
    ciphertext = ''  
    for x in groups:  
        c = self.rounds(x, self.subkey)  
        ciphertext += hex(int(c, 2))[2:].zfill(32)  
    return ciphertext

设轮函数为 $f (X_{i}, X_{i + 1}, X_{i + 2}, X_{i + 3}, r k_{i}) = X_{i} \oplus T (X_{i + 1} \oplus X_{i + 2} \oplus X_{i + 3} \oplus r k_{i})$
其中 $T (X) = L (S (X_{0}), S (X_{1}), S (X_{2}), S (X_{3}))$
$L (X) = X \oplus (X <<< 2) \oplus (X <<< 10) \oplus (X <<< 18) \oplus (X <<< 24)$
整轮的变换为 $τ_{i} (X_{i}, X_{i + 1}, X_{i + 2}, X_{i + 3}) = (X_{i + 1}, X_{i + 2}, X_{i + 3}, f (X_{i}, X_{i + 1}, X_{i + 2}, X_{i + 3}, r k_{i}))$
最终结尾处的交叉互换为 $σ (X_{32}, X_{33}, X_{34}, X_{35}) = (X_{35}, X_{34}, X_{33}, X_{32})$

def L(self, x: int) -> int:  
    return x ^ ((x<<2)&0xffffffff) ^ ((x<<10)&0xffffffff) ^ ((x<<18)&0xffffffff) ^ ((x<<24)&0xffffffff)  
  
def T(self, x: int) -> int:  
    x = hex(x)[2:].zfill(8)  
    X = [x[i:i + 2] for i in range(0, 8, 2)]  
    for i in range(4):  
        X[i] = self.Sbox(X[i])  
    return self.L(int(''.join(X), 16))

简写的话就是：
$f (a, b, c, d, k) = a \oplus T (b \oplus c \oplus d \oplus k)$
$τ_{i} (a, b, c, d) = (b, c, d, f (a, b, c, d, r k_{i}))$
$σ (a, b, c, d) = (d, c, b, a)$

完整的加密流程如下：
$Y = E_{K} (X) = σ \circ τ_{31} \circ τ_{30} \circ \dots \circ τ_{1} \circ τ_{0} (X)$

# 32轮轮函数
def rounds(self, text: str, subkey: list) -> str:  
    if len(text) < 128:  
        text = text.zfill(128)  
  
    X = [text[i:i + 32] for i in range(0, 128, 32)]  
    x = [int(X[i], 2) for i in range(4)]  
  
    for i in range(32):  
        tmp = x[0] ^ self.T(x[1] ^ x[2] ^ x[3] ^ subkey[i])  
        x = [x[1], x[2], x[3], tmp]  
  
    c = ''.join([bin(v)[2:].zfill(32) for v in [x[3], x[2], x[1], x[0]]])  
    return c

解密流程如下：
对加密函数求逆，得到
$X = E_{K}^{- 1} (Y) = (τ_{0}^{- 1} \circ τ_{1}^{- 1} \circ \dots \circ τ_{30}^{- 1} \circ τ_{31}^{- 1} \circ σ^{- 1}) (Y)$

接下来我们需要考虑 $τ_{k}^{- 1}$ 等于什么
$f$ 函数将第一个值异或了一个算出来的值，然后 $τ_{k}$ 进行了换位
所以要还原这第一个值，就需要先换位，然后再次异或原来那个值
即 $τ_{k}^{- 1} = σ \circ τ_{k} \circ σ$
换句话说， $σ \circ τ_{k}^{- 1} \circ σ \circ τ_{k}$ 是恒等变换

而 $σ \circ σ$ 也是恒等变换
因此， $X = σ \circ τ_{0} \circ σ \circ σ \circ τ_{1} \circ σ \circ \dots \circ σ \circ τ_{30} \circ σ \circ σ \circ τ_{31} \circ σ \circ σ (Y)$
$= σ \circ τ_{0} \circ τ_{1} \circ \dots \circ τ_{30} \circ τ_{31} (Y)$

故解密流程和加密流程是完全相同的，只是轮密钥顺序相反
这一点和DES等算法是一样的

# 解密函数
def decrypt(self, ciphertext: str) -> str:  
    text = bin(int(ciphertext, 16))[2:]  
    if len(text) % 128 != 0:  
        text = text.zfill((len(text) // 128 + 1) * 128)  
  
    groups = self.group(text)  
    plaintext = ''  
    inv_subkey = self.subkey[::-1]  
    for x in groups:  
        c = self.rounds(x, inv_subkey)  
        plaintext += hex(int(c, 2))[2:].zfill(32)  
    return plaintext

密钥拓展

该算法需要 128 bit 的种子密钥，将其拓展生成32个 32 bit 的子密钥/轮密钥

流程中用到的各参数如下：
系统参数 $F K = (F K_{0}, F K_{1}, F K_{2}, F K_{3})$
固定参数 $C K = (C K_{0}, C K_{1}, C K_{2}, C K_{3})$

轮密钥的生成方式与轮函数类似：
将种子密钥表示为 $(M K_{0}, M K_{1}, M K_{2}, M K_{3})$
计算 $(K_{0}, K_{1}, K_{2}, K_{3}) = M K \oplus F K = (M K_{0} \oplus F K_{0}, M K_{1} \oplus F K_{1}, M K_{2} \oplus F K_{2}, M K_{3} \oplus F K_{3})$
第 $i$ 个轮密钥 $r k_{i} = K_{i + 4} = K_{i} \oplus T^{'} (K_{i + 1} \oplus K_{i + 2} \oplus K_{i + 3} \oplus C K_{i})$
其中 $T^{'} (X) = L^{'} (τ (X))$
$τ$ 和轮函数里的一样
$L^{'} (X) = X \oplus (X << 13) \oplus (X << 23)$

  # 密钥扩展算法
  def genKey(self) -> list:  
    k0 = self.seedkey  
    rk = [0 for _ in range(32)]  
    MK = [int(k0[i:i + 32], 2) for i in range(0, 128, 32)]  
    K = [MK[i] ^ self.FK[i] for i in range(4)]  
    for i in range(32):  
        k = K[0] ^ self.T2(K[1] ^ K[2] ^ K[3] ^ self.CK[i])  
        K = [K[1], K[2], K[3], k]  
        rk[i] = k  
    return rk

总代码示例

import random  
  
class SM4:  
    FK = [  
        0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc  
    ]  
  
    CK = [  
        0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,  
        0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,  
        0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,  
        0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,  
        0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,  
        0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,  
        0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,  
        0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279  
    ]  
  
    S_box = [  
        ['d6', '90', 'e9', 'fe', 'cc', 'e1', '3d', 'b7', '16', 'b6', '14', 'c2', '28', 'fb', '2c', '05'],  
        ['2b', '67', '9a', '76', '2a', 'be', '04', 'c3', 'aa', '44', '13', '26', '49', '86', '06', '99'],  
        ['9c', '42', '50', 'f4', '91', 'ef', '98', '7a', '33', '54', '0b', '43', 'ed', 'cf', 'ac', '62'],  
        ['e4', 'b3', '1c', 'a9', 'c9', '08', 'e8', '95', '80', 'df', '94', 'fa', '75', '8f', '3f', 'a6'],  
        ['47', '07', 'a7', 'fc', 'f3', '73', '17', 'ba', '83', '59', '3c', '19', 'e6', '85', '4f', 'a8'],  
        ['68', '6b', '81', 'b2', '71', '64', 'da', '8b', 'f8', 'eb', '0f', '4b', '70', '56', '9d', '35'],  
        ['1e', '24', '0e', '5e', '63', '58', 'd1', 'a2', '25', '22', '7c', '3b', '01', '21', '78', '87'],  
        ['d4', '00', '46', '57', '9f', 'd3', '27', '52', '4c', '36', '02', 'e7', 'a0', 'c4', 'c8', '9e'],  
        ['ea', 'bf', '8a', 'd2', '40', 'c7', '38', 'b5', 'a3', 'f7', 'f2', 'ce', 'f9', '61', '15', 'a1'],  
        ['e0', 'ae', '5d', 'a4', '9b', '34', '1a', '55', 'ad', '93', '32', '30', 'f5', '8c', 'b1', 'e3'],  
        ['1d', 'f6', 'e2', '2e', '82', '66', 'ca', '60', 'c0', '29', '23', 'ab', '0d', '53', '4e', '6f'],  
        ['d5', 'db', '37', '45', 'de', 'fd', '8e', '2f', '03', 'ff', '6a', '72', '6d', '6c', '5b', '51'],  
        ['8d', '1b', 'af', '92', 'bb', 'dd', 'bc', '7f', '11', 'd9', '5c', '41', '1f', '10', '5a', 'd8'],  
        ['0a', 'c1', '31', '88', 'a5', 'cd', '7b', 'bd', '2d', '74', 'd0', '12', 'b8', 'e5', 'b4', 'b0'],  
        ['89', '69', '97', '4a', '0c', '96', '77', '7e', '65', 'b9', 'f1', '09', 'c5', '6e', 'c6', '84'],  
        ['18', 'f0', '7d', 'ec', '3a', 'dc', '4d', '20', '79', 'ee', '5f', '3e', 'd7', 'cb', '39', '48']  
    ]  
  
    def __init__(self, seedkey: str) -> None:  
        self.seedkey = seedkey  
        self.subkey = self.genKey()  
  
    def Sbox(self, x: str) -> str:  
        line = int(x[0], 16)  
        col = int(x[1], 16)  
        return self.S_box[line][col]  
  
    def L(self, x: int) -> int:  
        return x ^ ((x<<2)&0xffffffff) ^ ((x<<10)&0xffffffff) ^ ((x<<18)&0xffffffff) ^ ((x<<24)&0xffffffff)  
  
    def L2(self, x: int) -> int:  
        return x ^ ((x<<13)&0xffffffff) ^ ((x<<23)&0xffffffff)  
  
    def T(self, x: int) -> int:  
        x = hex(x)[2:].zfill(8)  
        X = [x[i:i + 2] for i in range(0, 8, 2)]  
        for i in range(4):  
            X[i] = self.Sbox(X[i])  
        return self.L(int(''.join(X), 16))  
  
    def T2(self, x: int) -> int:  
        x = hex(x)[2:].zfill(8)  
        X = [x[i:i + 2] for i in range(0, 8, 2)]  
        for i in range(4):  
            X[i] = self.Sbox(X[i])  
        return self.L2(int(''.join(X), 16))  
  
    # 密钥扩展算法  
    def genKey(self) -> list:  
        k0 = self.seedkey  
        rk = [0 for _ in range(32)]  
        MK = [int(k0[i:i + 32], 2) for i in range(0, 128, 32)]  
        K = [MK[i] ^ self.FK[i] for i in range(4)]  
        for i in range(32):  
            k = K[0] ^ self.T2(K[1] ^ K[2] ^ K[3] ^ self.CK[i])  
            K = [K[1], K[2], K[3], k]  
            rk[i] = k  
        return rk  
  
    # 32轮轮函数  
    def rounds(self, text: str, subkey: list) -> str:  
        if len(text) < 128:  
            text = text.zfill(128)  
  
        X = [text[i:i + 32] for i in range(0, 128, 32)]  
        x = [int(X[i], 2) for i in range(4)]  
  
        for i in range(32):  
            tmp = x[0] ^ self.T(x[1] ^ x[2] ^ x[3] ^ subkey[i])  
            x = [x[1], x[2], x[3], tmp]  
  
        c = ''.join([bin(v)[2:].zfill(32) for v in [x[3], x[2], x[1], x[0]]])  
        return c  
  
    # 分组函数，使用ECB模式  
    def group(self, text: str) -> list:  
        if len(text) % 128 != 0:  
            text = text.ljust((len(text) // 128 + 1) * 128, '0')  
  
        groups = [text[i:i + 128] for i in range(0, len(text), 128)]  
        return groups  
  
    # 总加密函数  
    def encrypt(self, plaintext: str) -> str:  
        text = bin(int(plaintext, 16))[2:]  
        if len(text) % 128 != 0:  
            text = text.zfill((len(text) // 128 + 1) * 128)  
  
        groups = self.group(text)  
        ciphertext = ''  
        for x in groups:  
            c = self.rounds(x, self.subkey)  
            ciphertext += hex(int(c, 2))[2:].zfill(32)  
        return ciphertext  
  
    # 解密函数  
    def decrypt(self, ciphertext: str) -> str:  
        text = bin(int(ciphertext, 16))[2:]  
        if len(text) % 128 != 0:  
            text = text.zfill((len(text) // 128 + 1) * 128)  
  
        groups = self.group(text)  
        plaintext = ''  
        inv_subkey = self.subkey[::-1]  
        for x in groups:  
            c = self.rounds(x, inv_subkey)  
            plaintext += hex(int(c, 2))[2:].zfill(32)  
        return plaintext  
  
  
# 调用示例  
if __name__ == "__main__":  
    alphabet = '0123456789abcdef'  
    # 用随机数据测试  
    seed = ''.join([random.choice(alphabet)for _ in range(32)])  # 128位密钥  
    print("seed key:", seed)  
    sm4 = SM4(bin(int(seed, 16))[2:].zfill(128))  
    num = random.randint(32,200)  
    plaintext = ''.join([random.choice(alphabet)for _ in range(num)])  
    print("plaintext:", plaintext)  
    ciphertext = sm4.encrypt(plaintext)  
    print("ciphertext:", ciphertext)  
    de_ciphertext = sm4.decrypt(ciphertext).lstrip('0')  
    print("decrypted ciphertext:", de_ciphertext)  
  
    if plaintext.lstrip('0') == de_ciphertext.lstrip('0'):  
        print("The codes run properly!")